Bundesliga-Experten sagen nicht nur, dass der Ball rund ist und das Spiel 90 Minuten dauert, sondern sie postulieren auch, dass 40 Punkte für den Klassenerhalt reichen.
Diese Weisheit wird so oft kolportiert, dass ich mich schon öfters gefragt habe, ob das eine fundamentale mathematische Gewissheit ist oder eine simple Faustregel. Sprich: reichen die 40 Punkte immer oder einfach nur üblicherweise.
Rechnerisch ist das nicht so leicht zu bewerkstelligen – ein Mathematiker in dem Bereich kann das sicherlich ohne Probleme, aber ich jedenfalls nicht. Zudem kann man bei solchen Dingen schnell in falschen logischen Schlüssen landen. Aber man kann es immer mit etwas simplem Ausprobieren angehen.
Da ich heute ausnahmsweise etwas Zeit habe, dachte ich mir, ich lasse das einfach von einem simplen Programm machen.
Wie simpel es sein darf, ist dabei schwer zu beurteilen. Schließlich ist die Bundesliga nicht die Ziehung der Lottozahlen – bestimmte Spielausgänge sind wahrscheinlicher als andere. So wird eine Mannschaft, die eine halbe Saison nur verloren hat, nicht plötzlich anfangen, jedes Spiel zu gewinnen. Heimspiele werden eher gewonnen als Auswärtsspiele.
Dennoch wollte ich es erst einmal mit dem simpelstmöglichen Modell versuchen. Dieses sieht so aus:
- Das Torverhältnis wird nicht beachtet. Schon alleine mit den drei Spielausgängen Gewonnen-Unentschieden-Verloren ist die Zahl der möglichen Saisonverläufe enorm. Eine Bundesligasaison hat 306 Spiele. Mit nur drei Spielausgängen landet man schon bei 3306 Möglichkeiten. Das entspricht ca. 10146
- Bei Punktgleichheit bestimmt der Zufall die Platzierung.
- Heimsieg, Auswärtssieg und Unentschieden sind gleich wahrscheinlich.
Ich ließ eine Million Saisons generieren mit einem recht guten Zufallsgenerator (für Programmierer: der libc-Zufallsgenerator stieß schon nach 8192 Saisons an seine Grenzen). Das dürfte auch in der Nähe dessen sein, was bei meiner technischen Lösung (PHP mit einer MySQL-Datenbank) überhaupt noch Sinn macht, denn alleine die Aufzeichnung der Endstände frisst so fast 1 Gigabyte Speicher. Zudem veränderten sich die Zahlen zum Schluss nur noch minimal – es müsste also eine ausreichende Stichprobe sein.
Das Ergebnis: in 80,7 % der Fälle reichten 40 Punkte für den Klassenerhalt. In diesem Szenario hat eine solche Leistung also eine sehr gute Chance – jedoch ist es keine Garantie, denn in knapp 20% der Fälle war mehr erforderlich. Es konnten sogar zwei Fälle gefunden werden, in denen 46 Punkte benötigt wurden. Diese zeichnet sich jedoch dadurch aus, dass die ganze Liga sehr ausgeglichen war und eben nur drei Mannschaften deutlich schlechter aussahen.
Umgekehrt reichten im Schnitt 59,1 Punkte für die Meisterschaft aus. Ab 50,3 Punkte gab es einen UEFA-Cup-Platz, wobei aber bis zu 60 Punkte benötigt werden können.
Während die Durchschnitte und Wahrscheinlichkeiten eine Aussagekraft haben, sind die anderen Angaben nicht absolut. So mag es sein, dass unter den unzähligen Saisonverläufen auch einer ist, der mehr als 46 Punkte für den Klassenerhalt benötigt. Es ist sogar relativ einfach, so einen zu konstruieren: wenn jeder Verein der Liga jeweils 17 Spiele gewinnt und 17 verliert, dann haben alle Vereine der Liga 51 Punkte. Hier wären also nicht einmal 51 Punkte eine Garantie für den Nichtabstieg. Freilich ein rein theoretisches Beispiel.
Um etwas realistischere Werte zu bekommen, habe ich das Verfahren so abgeändert, dass 50% aller Spiele mit Heimsiegen enden, 25% mit Auswärtssiegen und 25% mit Unentschieden. Das ist nicht abwegig, denn laut Wikipedia waren in der Saison 07/08 ganze 46,7% aller Spiele Heimsiege, während jeweils rund ein Viertel der Spiele auf Auswärtssiege und Unentschieden entfielen.
Wenn man diese Verteilung berücksichtigt, sollte die Simulation also etwas realistischer werden. Allerdings lässt sie nach wie vor außer Acht, dass nicht jede Mannschaft eine gleich große Chance hat, einen Auswärtssieg zu erringen.
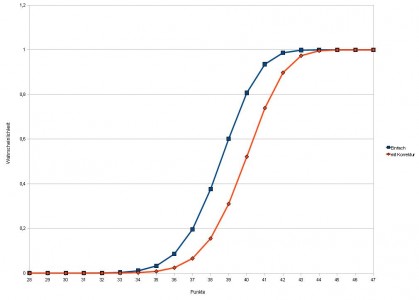
Wahrscheinlichkeit, mindestens Platz 15 zu erreichen in Abhängigkeit von der Punktzahl.
Dennoch sind die Ergebnisse interessant. Zum Einen steigen die jeweiligen Punktzahlen für die Plätze um einen Punkt an – was kein Wunder ist, weil Unentschieden erheblich seltener werden. Das betrifft auch die 40 Punkte. Sie reichen hier gerade einmal zu einer gut 50%igen Chance auf Klassenerhalt.
Dies widerspricht wiederum den Erfahrungen aus der Realität, die eher weniger als 40 Punkte nahelegen. Um solche Korrekturen anzubringen, braucht man also vermutlich mehr Details über Details und die Dynamik einer Bundesligasaison.
Der Schluss lautet also, dass 40 Punkte keineswegs eine Versicherung sind, aber in jedem Falle eine gute Chance geben.
Wie groß diese ist, ist freilich schwer zu bestimmen. Bis die Bundesliga 1 Million Saisons gespielt haben wird, kann man sich darüber Gedanken machen.
Naja,
die Regel will ja auch nur besagen, dass im real existierenden deutschen Profi Fussball noch niemand mit 40 Punkten abgestiegen ist (3-Punkte Regel, 18 Mannschaften). Am nächsten dran gekommen ist meiner Meinung nach 2005 Eintracht Trier, als die Mannschaft mit 39 Punkten aus der Zweiten Liga abgestiegen ist. Eigentlich hatte der KSC fünf Minuten vor Ende der Partie einen weiteren Treffer im Spiel gegen Cottbus erziehlt, dem der Schiri Drees jedoch fälschlicherweise die Anerkennung versagte. So stieg Trier (und nicht Cottbus) ab, im Folgejahr stieg Cottbus wieder in die Bundesliga auf und Trier stieg nochmals ab. Das war bitter, Eintracht Trier hat sich bis heute nicht erholt (zur Zeit abstiegsgefährdet in der Regionalliga).
Mit blau-schwarz-weissen Grüssen
Raffe
Nach etwas nachträglicher Überlegung bin ich auch zum Schluss gekommen, dass die Fragestellung so nicht ganz richtig ist, weil man ja leicht Fälle konstruieren kann, bei denen man 51 Punkte zum Klassenerhalt braucht. Es kommt also am Ende darauf an, wie wahrscheinlich Fälle über den 40 Punkten sind. Vielleicht hätte ich bei der Analyse auch lieber Platz 16 betrachten sollen, denn selbst wenn der 15. Platz 40 Punkte hat, heißt das ja nicht, dass er diese gebraucht hat – der 16. kann ja nur 38 Punkte gehabt haben. Letzlich zeigt die Analyse nur, dass die Wahrscheinlichkeit des Klassenerhalts irgendwo um die 39 Punkte so massiv ansteigt, dass ein Abstieg kaum noch vorkommen wird. Ich denke, der tiefergehende Grund dafür, dass in der Realität eher weniger gebraucht werden, ist, dass das Feld relativ ungleichmäßig ist. Meine Simulation geht ja davon aus, dass jede Mannschaft mit gleichen Chancen startet, und das ist definitiv nicht der Fall.
Von der in der Fußballwelt beliebten Dramatisierung der letzten Spieltage halte ich allerdings nicht so viel. Wenn eine Mannschaft am letzten Spieltag noch eine realistische Chance hat, den Klassenerhalt zu schaffen, dann ist das zwar schön, aber man sollte dabei nicht aus dem Auge verlieren, dass ein Abstiegsplatz das Ergebnis einer schlechten Saison ist und nicht eines einzigen Spiels. Auch den Schiri anzuprangern ist da leicht, aber im Laufe der 306 Spiele werden so viele Fehler durch die Schiris gemacht, dass man das Endergebnis unmöglich auf einen schieben kann.
Bei deinem Beispiel besteht auch das Problem, dass es sich auf die 2. Liga bezieht. Eintracht Trier erreichte einen 15. Platz, der in der 1. Liga für den Klassenerhalt reichen würde. Als Beispiel würde ich da eher die Saison 2003/2004 heranziehen:
http://de.wikipedia.org/wiki/2._Fu%C3%9Fball-Bundesliga_2003/04
Da lagen Platz 15 und 16 bei 39 Punkten. Um also nicht aufs Torverhältnis angewiesen zu sein, musste man da also wirklich 40 Punkte haben.
trotzdem sehr coole Üerlegungen, vor allem auch die theoretisch Grenze von 51 Punkten.
Theoretisch könnte man mit 57 Punkten absteigen. Zwei Mannschaften verlieren alle Spiele (außer dem gegeneinander). Alle anderen Mannschaften gewinnen ihre Heimspiele und die Auswärtsspiele gegen die beiden Verlierermannschaften. Dann haben am Ende 16 Mannschaften 19*3=57 Punkte. Ist natürlich nur ein rein theoretischer Fall.
Aber eine Lehre kann man trotzdem ziehen: Auch eine Millionen Simulationen reichen bei weitem nicht aus, um alle möglichen Szenarien durchzuspiel.:-)
Danke für den Link und den Hinweis. Interessiert, dass diese kleine Spielerei solche Kreise zieht.
Wie in dem Mathematikbeitrag angemerkt, ist die Zahl der Fälle gewaltig groß. Selbst wenn man berücksichtigt, dass man die Namen der Vereine beliebig vertauschen kann, landet man immer noch bei 10143 Saisonverläufen. Das könnte man nicht durchrechnen, selbst wenn alle Computer der Welt seit dem Urknall daran gearbeitet hätten.
Den beschriebenen Ausgang mit 57 Punkten kann man ja auch erreichen, wenn man Auswärts- und Heimsieg bei einer oder mehreren Vereinskombinationen (außer den Verlierermannschaften) vertauscht. Hierdurch entstehen ca. 1040 Saisonverläufe mit diesem Ergebnis. Das klingt nach viel, ist es aber nicht, denn die Wahrscheinlichkeit, dass ich mit meiner Simulation eine davon erwischt hätte, wäre dann immer noch ca. 1:10103.
Es ist also nicht unmöglich, aber so überragend unwahrscheinlich, dass es nie auftreten würde.
Quelle: http://www.mathematik.de/ger/presse/ausdenmitteilungen/artikel/mdmv-19-3-153.pdf