Es ist eine Art Fußballweisheit: bei den großen Turnieren ist man raus, wenn man zweimal verloren hat. Wenn man zweimal gewonnen hat, ist man weiter. Unter 4 Punkten kann man das Weiterkommen gleich vergessen.
Ich habe mich gefragt: ist das wirklich so?
Die Aufgabe ist überschaubar – es sind 6 Partien, die in einer Gruppe gespielt werden. Da es drei verschiedene Resultate gibt (Sieg 1. Mannschaft, Unentschieden, Sieg 2. Mannschaft), gibt es 6 hoch 3 Spielausgänge, also 729 Kombinationen.
Dabei gilt zu beachten, dass dies nur gilt, wenn man die vier Teams eindeutig festlegt. Rein kombinatorisch sind viele doppelt. Zur Erklärung: wenn man vier Teams A,B,C und D hat und alle Unentschieden spielen bis auf die Partie A gegen B, dann ist die Tabelle identisch mit dem Fall, dass alle Unentschieden spielen bis auf die Partie C gegen D. Man muss lediglich die Teamnamen tauschen und landet bei derselben Tabelle.
Letztlich gibt es 40 verschiedene Tabellen, d.h. 40 verschiedene Punktekombinationen.
Wenn man das also außer Acht lässt und mit vier festgelegten Teams alle Varianten durchspielt, kommt man zu folgendem Ergebnis:
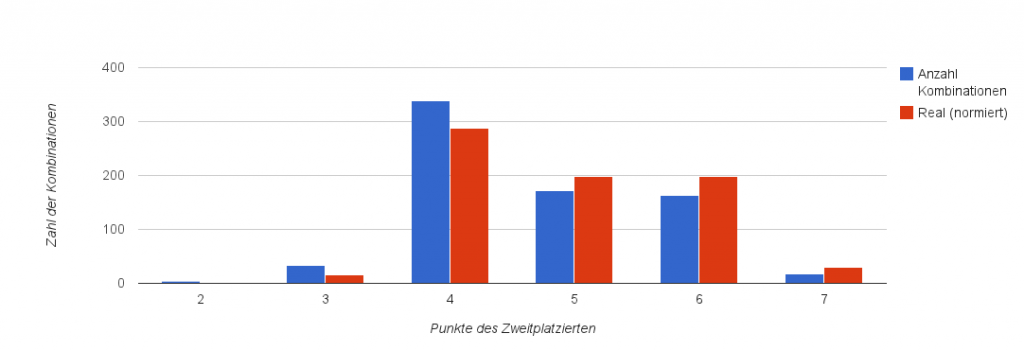
Für die roten Balken habe ich die Weltmeisterschaften seit 1998 und die Europameisterschaften seit 1996 ausgewertet. Nur bei diesen Wettbewerben musste man zwingend Gruppenzweiter werden, um weiterzukommen. Außerdem galt davor die Zweipunkteregel.
Das Ergebnis aus den 48 Gruppen, die es bislang in der Form gab:
- Zweimal hatte der Zweitplatzierte 7 Punkte. Es ist aber nicht so, dass man sie gebraucht hätte, denn auch ein Blick in die reine Kombinatorik zeigt: das kommt nur zustande, wenn die zwei stärksten Teams gegeneinander Unentschieden spielen und die jeweils anderen beiden Teams besiegen. Für die anderen beiden Teams bleiben also nur noch die Punkte des Spiels gegeneinander übrig, wodurch der Drittplatzierte maximal 3 Punkte haben kann.
- 13 mal hatte der Zweitplatzierte 6 Punkte
- Ebenfalls 13 mal hatte der Zweitplatzierte 5 Punkte.
- Ganze 19 mal reichten dem Zweitplatzierten 4 Punkte. In der Kombinatorik ist das aber noch eine relativ riskante Kombination: in 40% der Fälle scheidet jemand mit 4 Punkten aus, aber deutlich über die Hälfte nur wegen des Torverhältnisses.
- Ein einziges Mal genügten sogar 3 Punkte. Das geht in der Tat nur, wenn jedes Team genau einmal gewinnt oder wenn ein Team besonders stark ist und die anderen sich gleichmäßig verteilen. Dieser Fall ergab sich für Chile bei der WM 1998. Vier der sechs Partien ging Unentschieden aus, so dass Chile dadurch weiter kam, dass sie gegen den Gruppenersten Italien nicht verloren.
- Nie gab es einen Fall, dass ein Team mit nur 2 Punkten weiter kam. Doch er ist möglich: wenn ein Team alle anderen besiegt (d.h. 9 Punkte) und alle anderen Teams untereinander nur Unentschieden spielt, dann hat der Gruppensieger 9 Punkte und alle anderen 2 Punkte. Freilich ein sehr exotischer Fall.
Letztere beiden Punkte dürften die einzigen Überraschungen sein, aber sie haben natürlich nur begrenzte reale Relevanz, denn kein Team spielt auf Unentschieden, und die Teamstärken sind selten so gleichmäßig verteilt, dass jede Mannschaft nur einziges Mal gewinnt.
Das rigorose Durchrechnen bestätigt letztendlich Selbstverständlichkeiten: mit drei Siegen ist man in jedem Fall Gruppensieger, und unter zwei Unentschieden kommt man nicht weiter. Ob einem ein Sieg und zwei Niederlagen reichen, kann man sich auch leicht ausknobeln: Nein, es geht nicht.
Bleibt noch die Frage, ob man mit zwei Siegen auch nicht weiterkommen kann. Erstaunlicherweise lautet die Antwort Ja, und zwar genau dann, wenn eine Mannschaft alle Spiele verliert und die anderen drei es sich so aufteilen, dass jede am Schluss genau 6 Punkte hat. Rein theoretisch reichen also auch zwei Siege nicht.
In der Praxis ist das freilich wohl noch nie aufgetreten. Daher gilt: wer zweimal verliert, ist raus. Wer zweimal gewinnt, ist nicht garantiert, aber mit größter Wahrscheinlichkeit weiter.
In diesem Sinne: heute abend einfach gewinnen.
Update 23:01 Uhr: Doof, wenn man sich selbst widerspricht – der gestrichene Satz weiter oben behauptet das Gegenteil von dem, was in der Auflistung steht. Noch blöder, wenn genau so etwas ausgerechnet jetzt passieren kann. Ein einziger Sieg (und zwei Niederlagen) können in der Tat reichen, um weiterzukommen. Entweder, wenn es dauernd unentschieden gibt, oder – wie jetzt in der Gruppe B eintreten kann – wenn eine Mannschaft alle anderen schlägt und die anderen drei jeweils einen Sieg einfahren. Sollten Deutschland und die Niederlande am Sonntag gewinnen, dann sind Niederlande, Portugal und Dänemark punktgleich. Der direkte Vergleich taugt dann auch nicht, so dass nur das Torverhältnis herhalten kann. Da noch nicht viele Tore gefallen sind, kann es da schnell eng werden. Es bleibt spannend.
Das ist ja mal wieder ein cooler Beitrag. Rechenspiele mit Fussball besser geht es ja gar nicht 😉
Und mit der Deutschland-Gruppe hast du auch gleich noch ein schönes Beispiel, da ja selbst DTLD noch mit 6 Punkten noch Dritter werden kann und NL mit nur 3 Punkten Zweiter.
„Außerdem galt davor die Zweipunkteregel“
Dazu ist zu sagen: diese extremen Kombinationen, zwei Siege reichen nicht zum Weiterkommen / ein Sieg reicht zum Weiterkommen, funktioniert mit der alten Zaehlweise genauso. Und ist auch passiert, naemlich bei der WM 1982 in Spanien: Deutschland gegen Oesterreich, das Skandalspiel. In der Abschlusstabelle hatten drei Teams 2x gewonnen und somit 4 Punkte jeweils. Algerien schied aus, weil das Spiel bereits gelaufen war, und Deutschland und Oesterreich genau wussten, wie sie spielen muessen, um Beide weiter zu kommen. Als Reaktion auf den Skandal wurde eingefuehrt, dass die letzten Gruppenspiele zeitgleich stattzufinden haben.
Ich habe spaßeshalber mal meine Analyse mit der Zweipunkteregel wiederholt.
Die Bandbreite nimmt erheblich ab dabei. Von den vormals 40 verschiedenen Schlusstabellen sind dann noch 16 übrig. In nur 18 der 729 Kombinationen hat der Zweitplatzierte fünf Punkte, wobei das aber nicht bedeutet, dass 4 nicht gereicht hätten, denn bei diesen Konstellationen haben zwei Teams 5 Punkte und die anderen beiden waren weit abgeschlagen, also ähnlich den Konstellationen im jetzigen System, wo zwei Teams vorne 7 Punkte haben. Wie zu erwarten ist ein Unentschieden erheblich mehr wert als bei der Dreipunkteregel. Ein Sieg und ein Unentschieden reichen bei 98% der Konstellationen zum Weiterkommen, während es beim Dreipunktesystem nur 51% sind.
Der von dir beschriebene Fall von 1982 kann wirklich nur eintreten, wenn eine Mannschaft alle Spiele verliert und sich die anderen die Siege gleichmäßig verteilen. Beim Dreipunktesystem hätten Deutschland, Österreich und Algerien jeweils 6 Punkte gehabt, so dass auch hier das Torverhältnis entschieden hätte. Insofern ist es auch gut, dass die Spiele nun gleichzeitig stattfinden, um solchen taktischen Spielen erst gar nicht den Boden zu bereiten.
Anzumerken wäre auch noch, dass die Situation in den WMs 1986, 1990 und 1994 nicht nur wegen der Zweipunkteregel anders gelagert ist, sondern auch wegen der Regel, dass die besten Drittplatzierten weiterkamen. Das macht die Sache noch komplexer, da nicht nur das reine Abschneiden innerhalb der Gruppe, sondern auch die Verhältnisse in anderen Gruppen eine Rolle spielte. Ab 2016 soll ein solches Verfahren auch bei der EM eingesetzt werden, was die Sache zumindest spannend machen wird.
„Da es drei verschiedene Resultate gibt (Sieg 1. Mannschaft, Unentschieden, Sieg 2. Mannschaft), gibt es 6 hoch 3 Spielausgänge, also 729 Kombinationen.“
6^3 = 6 * 6 * 6 = 216
3^6 = 3*3*3*3*3*3 = 729
Ich glaube 3 hoch 6 ist richtig.
Ich meinte 3 hoch 6 ist nicht richtig (also 729) sondern 216